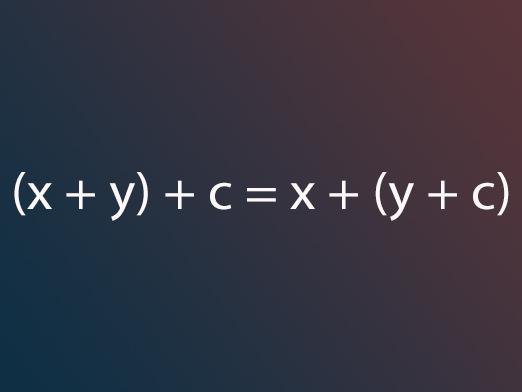Pravidla pro přidávání vektorů

Pro provedení operace přidávánívektory, existuje několik způsobů, které mohou být v závislosti na situaci a typu uvažovaných vektorů pohodlnější. Podívejme se na pravidla přidávání vektorů:

Pravidlo trojúhelníku

Pravidlo trojúhelníku je následující: pro přidání dvou vektorů x, y je nutné konstruovat vektor x tak, že jeho původ se shoduje s koncem vektoru y. Pak jejich součet bude hodnota vektoru z a počátek vektoru z se shoduje se začátkem vektoru x a konec s koncem vektoru y.

Pravidlo trojúhelníku pomáhá, pokud počet vektorů, které je třeba sčítat, není větší než dva.

Pravidlo pro mnohoúhelník

Pravidlo polygonu je nejjednodušší a nejpohodlnějšípřidat libovolný počet vektorů v rovině nebo ve vesmíru. Podstata pravidla je následující: při přidávání vektorů je třeba postupně zarovnat je po jednom tak, aby se začátek následujícího vektoru shodoval s koncem předchozího vektoru a vektor, který uzavře formovanou křivku, je součtem pojmů vektorů. Toto je graficky znázorněno rovnicí w = x + y + z, kde vektor w je součtem těchto vektorů. Navíc je třeba poznamenat, že součet se nemění se změnou v místech pojmů vektorů, tj. (X + y) + z = x + (y + z).

Pravidlo rovnoběžníku

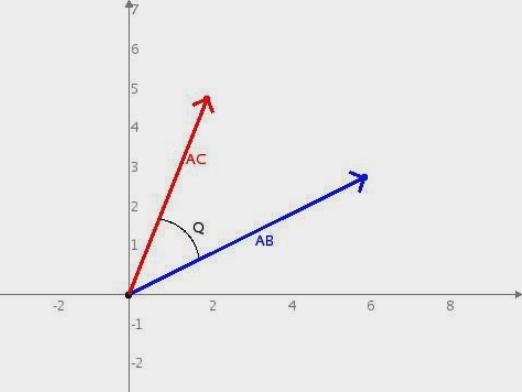
Pravidlo paralelogramu se používá k přidánívektorů, které pocházejí z jediného bodu. Toto pravidlo říká, že součet vektorů x a y, která má počátek v jednom bodě bude Třetí směr Z, pocházející také z tohoto bodu, a vyznačující se tím, že vektory x a y jsou strany rovnoběžníku, a vektor z - jeho diagonální. Také v tomto případě nezáleží na tom, budou tyto vektory být vytvořeny v libovolném pořadí.

Pravidlo pro mnohoúhelníky, pravidlo trojúhelníku a pravidlo pro rovnoběžníky pomáhají vyřešit problém s přidáním vektorů absolutní složitosti jak v rovině, tak ve vesmíru.