Jak najít základ trojúhelníku?

Geometrie je jedním ze školních předmětůužitečné v budoucnosti pro všechny. Z jednoduchého důvodu - geometrie a pozdější stereometrie rozvíjí prostorové myšlení. A pokud budeme chápat zákony, na kterých je vybudován samotný Vesmír, bude snazší pochopit jiné, mnohem zajímavější věci, které v tomto prostoru fungují.

Obecný případ

Ale zpět k našim trojúhelníkům. Začneme tím, že se odchylujeme od podrobností a uvidíme, jak najít základ trojúhelníku, který není ani rovnostranný, ani rovnoramenný ani obdélníkový. Vzhledem k tomu, že jakákoli strana může sloužit jako základ v takové osobě, pro začátečníky budeme volit obličej a "zavolat" na základ. Podle toho otočte trojúhelník tak, aby byl na něm, a budeme hledat jeho délku.

V tom pomůžeme slavnou větu kosinů,jehož zvláštním případem je Pythagorova věta. Kosinová věta uvádí, že čtverec jedna strana trojúhelníku se rovná součtu ostatních dvou trojúhelníku stranách, předem kvadratických minus produktů z těchto stran násobí dvěma a vynásobených kosinu úhlu mezi nimi. Pokud je známo, délka dvou stranách a úhlu mezi nimi, přičemž náhrada je ve vzorci a je problém vyřešen. V případě, že údaje se liší od toho, že je třeba snížit výšku základny, který má dvě pravoúhlé trojúhelníky. No, jak najít základ pravého trojúhelníku je triviální úkol. poměry stran a úhlů nám umožňují vypočítat délku základny s minimálními údaji. Jelikož úkoly v učebnicích musí být vyřešeny, vše se ukáže.

Je rovnoměrný trojúhelník

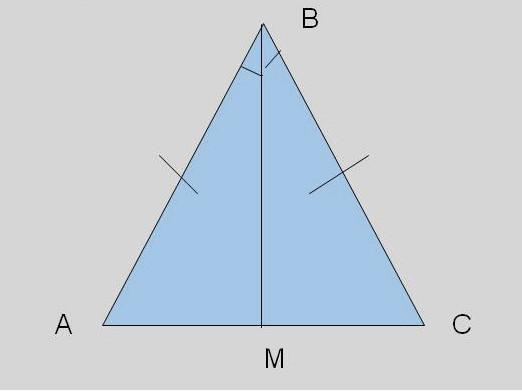
Zjednodušujeme úkol. U některých úloh je trojúhelník dán jako rovnoměrný. Připomeňme si, že rovnoměrný trojúhelník má dvě stejné strany. Báze bude považována za třetí stranu. Jak najít v tomto případě základy rovnoramenného trojúhelníku? Bude nutné znát jednu stranu a úhel naproti základně. Vzhledem k tomu, že boky jsou stejné - druhá strana je známá a rovná se první. A pak cosiinovou teorémem stále nalezneme základ.

Obdélníkový trojúhelník

Pohádka pro žáka. Obdélníkový, to je trojúhelník s úhlem devadesát stupňů - nejvhodnější trojúhelníku. Jak najít délku základny trojúhelníka s pravým úhlem - otázku, která pomůže najít poměr stran jiných, než pravoúhlé trojúhelníky. Další úkoly jsou často snížena na to tím, že drží výšky trojúhelníku, který dělí postavu do dvou pravoúhlých trojúhelníků. Zde vstoupí v platnost zvláštní případ kosinové věty - pythagorské věty. Vzhledem k tomu, kosinus pravého úhlu je rovna nule, vedlejší produkt mizí, přičemž na pravé straně pouze součet čtverců na nohou, na levé straně rovnice je čtverec přepony - strana protilehlá pravém úhlu. A proto může být základem pravého trojúhelníku nějaká jeho noha.

Rovnoběžný trojúhelník

Jak najít základ rovnostranného trojúhelníku- otázka, obecně řečeno, neobvyklá. K vyřešení tohoto "složitého" problému je třeba znát délku alespoň jedné strany trojúhelníku. A protože všechny strany trojúhelníku jsou stejné (rovnostranné) - základna bude rovna délce strany. Tento problém je spíše vtipný než znalost geometrie.